What does it mean to reason in AI?

By end of the first VQA challenge, most researchers agreed that the reasoning capabilities of the first generation VQA models were fairly limited or non-existent. Now a new wave of models are flooding the market which attempt to address this issue. Learning to Reason, Inferring and Executing Programs for Visual Reasoning, and Relation Networks are few examples of these next generation models. In many of these papers, authors do not explicitly define reasoning since what they intend to convey is often clear from context and the examples in the papers. However reasoning is a farily complex concept with many flavors and interesting connections to psychology, logic, and pattern recognition. This warrants a more thorough discussion about what it means to reason in the realm of AI and that’s what this post is all about.
What does it mean to reason in layman’s terms?
A reason is any justification intended to convince fellow human beings of the correctness of our actions or decisions.
In other words, if the sequence of steps or arguments you used to reach a certain conclusion were shown to other people and they reached the same conclusion without questioning any of the arguments, then your reasons have held their ground. Note that what counts as a valid reason is often context-dependent. For instance, consider justifying calling a person crazy. When used in social context, say during an argument with a friend, divergence from commonly expected behaviour or established norms of morality is a valid reason. But these arguments without a clinical diagnosis do not hold any merit in the courthouse of clinical psychology.
When would we call an AI agent to be capable of reasoning?
Applying the layman’s definition, let us ask the question - What would convince us of a machine’s actions or help us accept the predictions coming from an AI system? Maybe the AI needs to be able to list out the steps of inference which humans can manually inspect and execute to reach the same prediction. But here’s a trick question -
Would we still call the agent capable of reasoning if inference consists of only a single step of pattern matching or look up in a database?
While it may seem counter-intuitive to some, using our definition of a reason above, I would like to argue that such an agent may still be said to reason in a particular domain of discourse if the following hold:
- the approach makes correct predictions for any input in the domain of discourse if the pattern matching is correctly executed,
- the agent defines the pattern matching criterion in a human understandable way that allows the item retrieved to be manually verified to be a correct match given the criterion, and
- given the definition of matching criterion, and a correct match a human makes the same prediction.

What this implies is that a QA system (as shown above) which only expects one of \(N\) questions, and answers them by matching the question string to a database of question strings paired with their correct answer string, could be called a reasoning system. This is because the system tells you exactly how it computed the answer in a way that can be manually verified (does the retrieved question string match the query question string) and executed to get the same answer. However, if we expand the domain of discourse to include a question that is not stored in the database, the system fails to produce an answer. Therefore, it is a brittle system which is pretty much useless for the domains of discourse that humans usually deal with or would like AI to deal with.
It is easy to build a system that reasons, just not one that works for a meaningfully large domain of discourse.
Reasoning, Pattern Recognition and Composition
Taking the table lookup approach to its extreme, any reasoning problem can be solved by a table lookup provided you could construct a python dictionary with keys as every possible query expected with their values being the corresponding outputs. There is a practical problem though (you think so Sherlock!). This dictionary in most AI applications would be gigantic if not infinitely large. Consider VQA for example. We would need to map every possible image in the world and every possible question that can be asked about it to an answer. People will definitely call you crazy for trying to pull off something like this. But this is where statistical pattern recognition and compositional nature of the queries comes to our rescue by helping us reduce the dictionary size.
Statistical Pattern Recognition
In QA a question may be posed in multiple ways using different syntax. For example,
Mary and John have been married for 5
years. Mary gave birth to a child an year after their marriage. How
old is the child now?
and
How old is Mary and John's child now if
Mary gave birth to the child the year after they got married? They got
married 5 years ago.
are semantically the same question but the strings are quite different. For most questions there are plenty of such semantic duplicates. One way to reduce the size of the dictionary is to store only one representative for each unique semantic sense and use statistical pattern recognition (SPR) for learning a semantic matcher instead of a simple string matcher. A naive way is encoding sentences using an RNN trained as a language model and using nearest neighbor lookups in the embedding space. But generally this won’t work nearly as well as we’d hope. This is where smart ways of encoding the sentence using parsing helps.
Composition
Composition may be though of as another aid to SPR. In the previous
example, we can replace the names Mary and John with any other
names but the meaning of the question relative to those names and its
answer doesn’t change. So the real challenge is to match the following
structure which is composed of different types of nodes and
edges. These elements combined together represent a unique semantic
sense.
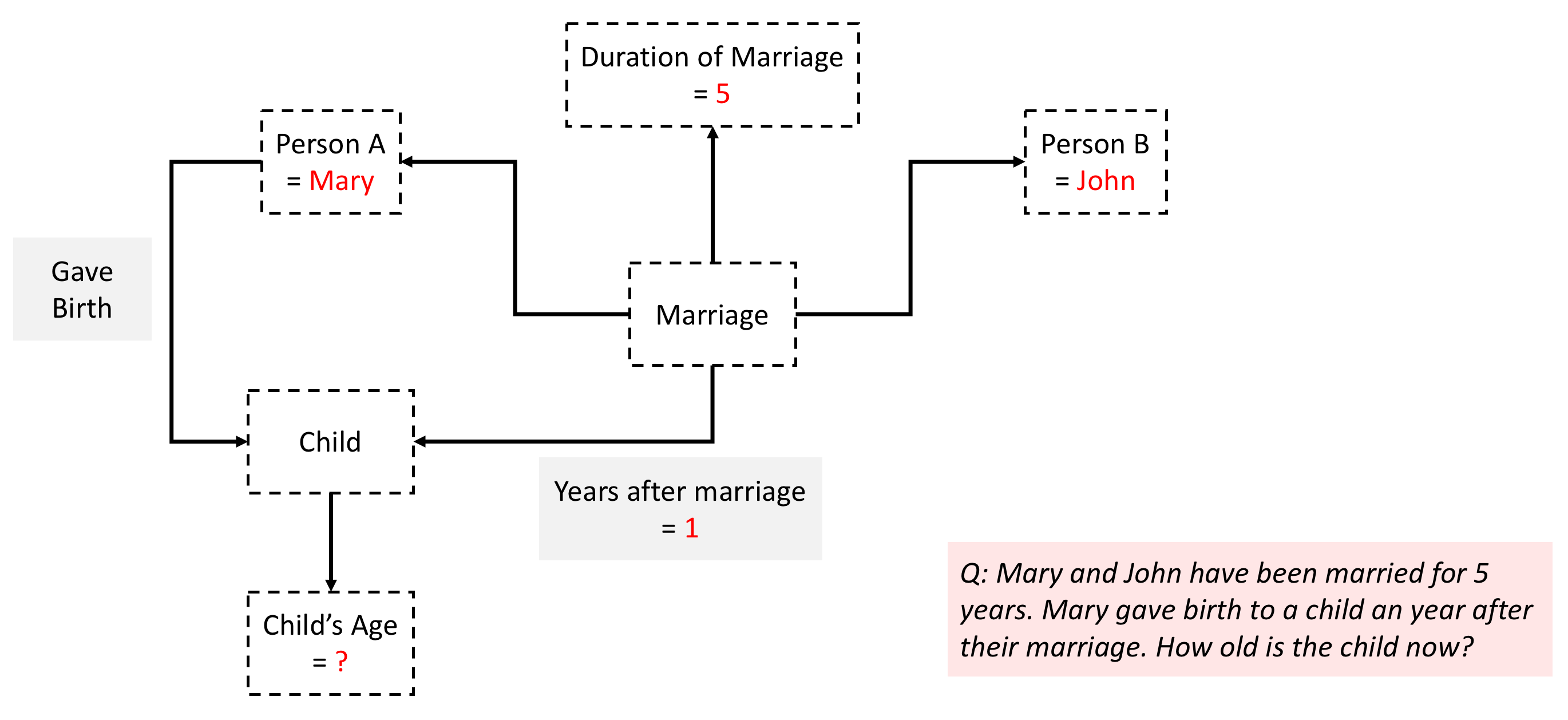
Further improving tractability through math and logic
So far, our lookup based approach would need to match a query to an
instantiation of this structure in terms of some or all of its
variables. For instance, in this case 5 years and 1 year are
instantiations of variables that are crucial for answering the
question. This means that in our database we need to have the question
and answer stored for every possible instantiation of variables
Duration of Marriage and Years after marriage. This observation
provides yet another opportunity for a reduction in the
dictionary size by recognizing that the answer is a formula or a
program that can be executed - Child's Age = Duration of Marriage -
Years after marriage. Useful math primitives include algebraic operators
(\(+,-,\times,\div\)), comparators (\(>,<,=\)), and logical
operators (\(\land,\lor,\neg\)). Now our inference consists of two
steps -
- match question structure in the database to retrieve the math or logical formula, and
- execute the formula on the instantiation provided by the query to get the answer.
Let’s talk implementation
Implementation of VQA systems based on some of the above ideas can be found in Learning to Reason and Inferring and Executing Programs for Visual Reasoning. Both works construct agents which given a question about an image list a sequence of steps, or a program if you will, that can be executed on an image to get the answer. Each consists of passing the image or a feature map through a neural module whose output is a feature map, an attention map, or an answer. Each neural module is dedicated to a certain task such as finding a particular object or attribute, counting, comparison etc. Once assembled the modules form a network that can be trained using backpropagation. This also leads to very efficient data usage for learning through module reuse across different questions.
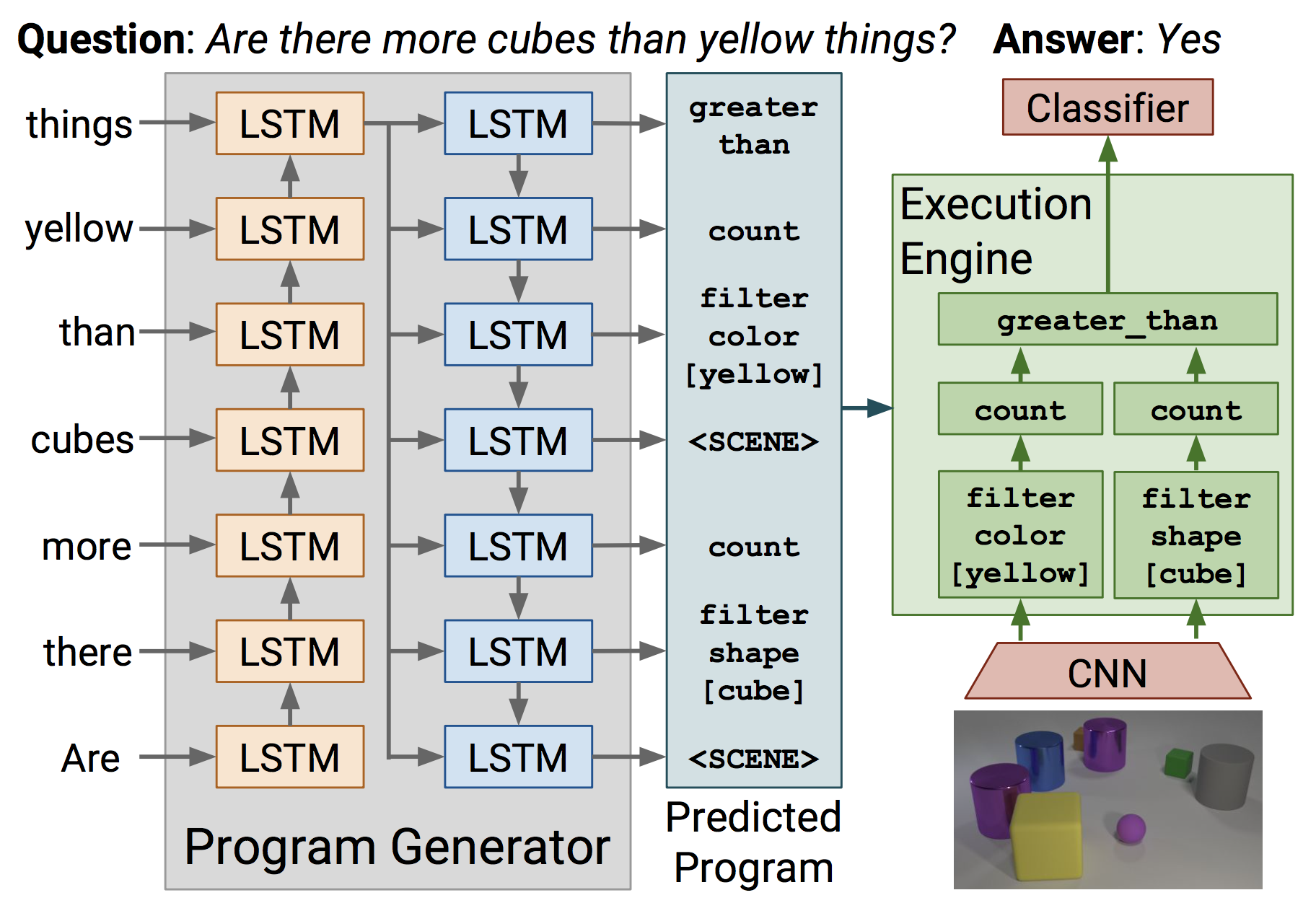
Limitations: While these models seem quite powerful and general
enough for a large class of questions, they are not perfect. One
issues is that these models need to relearn any math or logical
operation from scratch while there is really no need to learn things
like greater_than using a neural network when most programming
languages provide > operator. Some of the operations that the
modules try to learn in a weakly supervised way, such as detection and
segmentation, have completely supervised datasets and fairly
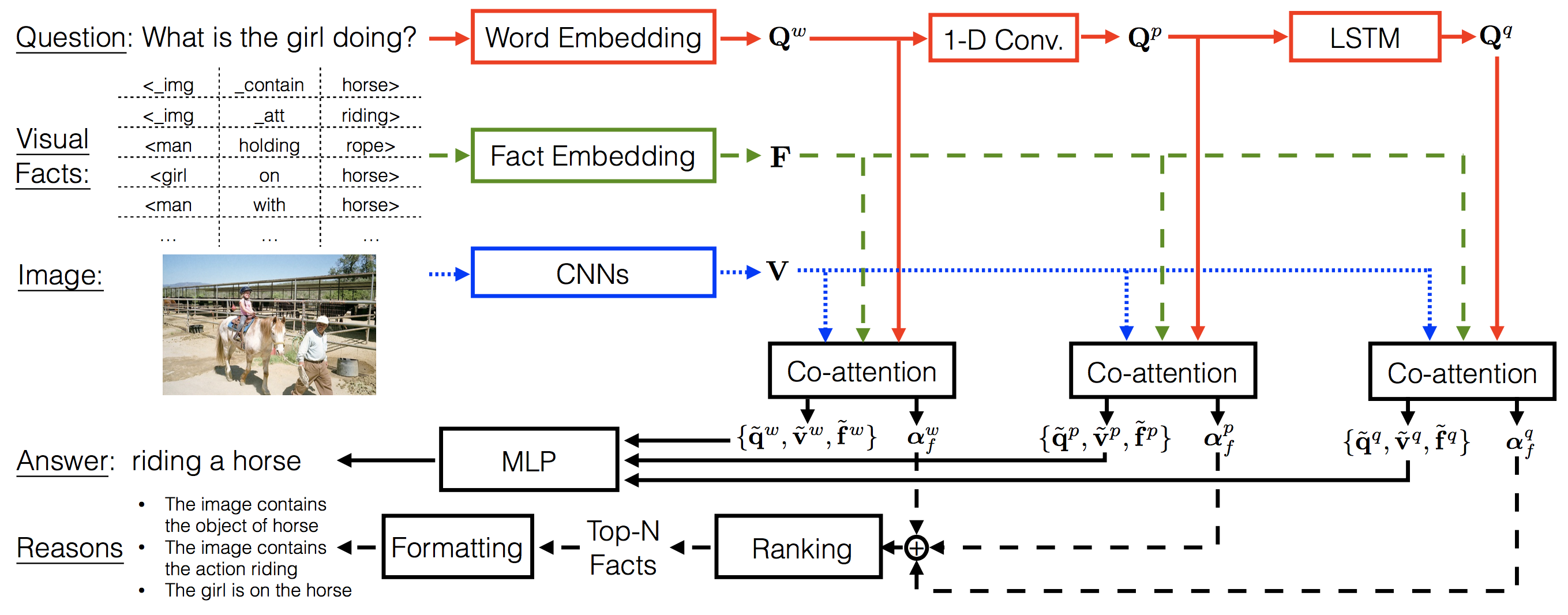
sophisticated models dedicated to these tasks alone. The VQA Machine:
Learning How to Use Existing Vision Algorithms to Answer New
Questions is a recent paper that
uses object, attribute and relationship predictions from specialized
and separately trained models as facts in VQA inference.
Another limitation of these models is that they need the agent that predicts the program to be jump started using some kind of imitation learning using ground truth programs during training which more often than not are hard to come by. Albeit once pretrained, the agents can be finetuned without ground truth programs using REINFORCE. Again these are reasoning models because humans can execute the program in our brains once we see an image and get the answer to the question.
Dynamic vs static composition
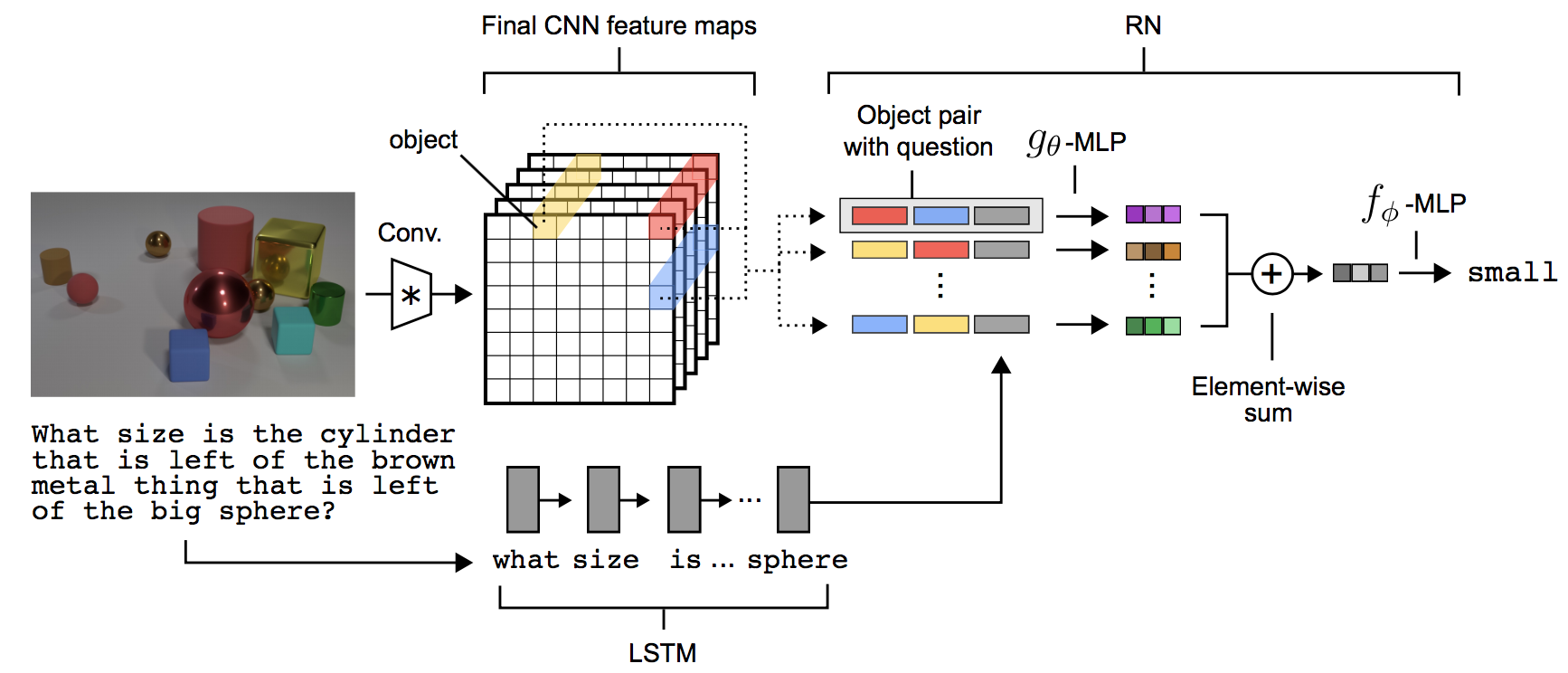
An important thing to remember here is that a model doesn’t necessarily have to be dynamic to be doing compositional reasoning. Sometimes the explanation we seek in a reasoning model is not instance specific or even explicit but rather baked into a static architecture. For example, Relation Networks are supposed to be doing relational reasoning but the model does not really provide any instance specific explanation for the predictions. However, the architecture is designed to do more than just single-shot, black-box whole image feature extraction and prediction. Instead the model looks at all possible pairs of regions, encodes each region-pair and question tuple using a shared module, pools these representations using element-wise sum, and finally makes an answer prediction using this image representation. Here the explanation for each prediction (and the reason why we would trust the prediction) is that for answering questions about relations of two objects, we would expect to get the right answer only by looking at pairs of objects, and that is built into this particular model’s inference but is not enforced in the first generation VQA models which perform abysmally on relational questions.
Logical rules in Reasoning
Logical operators are not the only thing that we can borrow from formal logic to improve tractability of learning. Logic sometimes also provides a way to encode rules and constrains learning. Since most of machine learning deals with probabilities, we also want to encode these rules as soft constraints. Probabilistic soft logic (PSL) is one way to do it. To get a flavor of PSL, let us try and encode modus ponens, which refers to the following logical rule in propositional logic
Note that this can be compactly written as
Now in PSL, \(A\) and \(B\) are not booleans but rather floating
values in the range \(\left[0,1\right]\), which could be predictions
coming from a network with sigmoid activation in the last layer. This
allows operations like \(\land\) and \(\rightarrow\) to be computed
using simple math operations such as
$A \lor B \implies \text{max}\{A+B,1\}$
$\neg A \implies 1-A$
$A \rightarrow B \implies \neg A \lor B \implies \text{max}\{1-A+B,1\}$
Using these modus ponens becomes
with corresponding colors denoting $(A
\land$$(A\rightarrow B)$$)$. This means that if we have probabilistic
truth values of $A$ and $B$, we can plug it into the above equation
and get a value between $[0,1]$ with $1$ indicating the rule being
exactly satisfied and $0$ indicating the rule not being satisfied at
all. Note that each branch of logic - propositional logic, predicate
logic etc. provides a bunch of these general rules of
inference. But depending on the problem, one may be able to come up
with specific logical rules. For example, an object detector might
find it useful to know that cats don’t fall from the sky (usually).
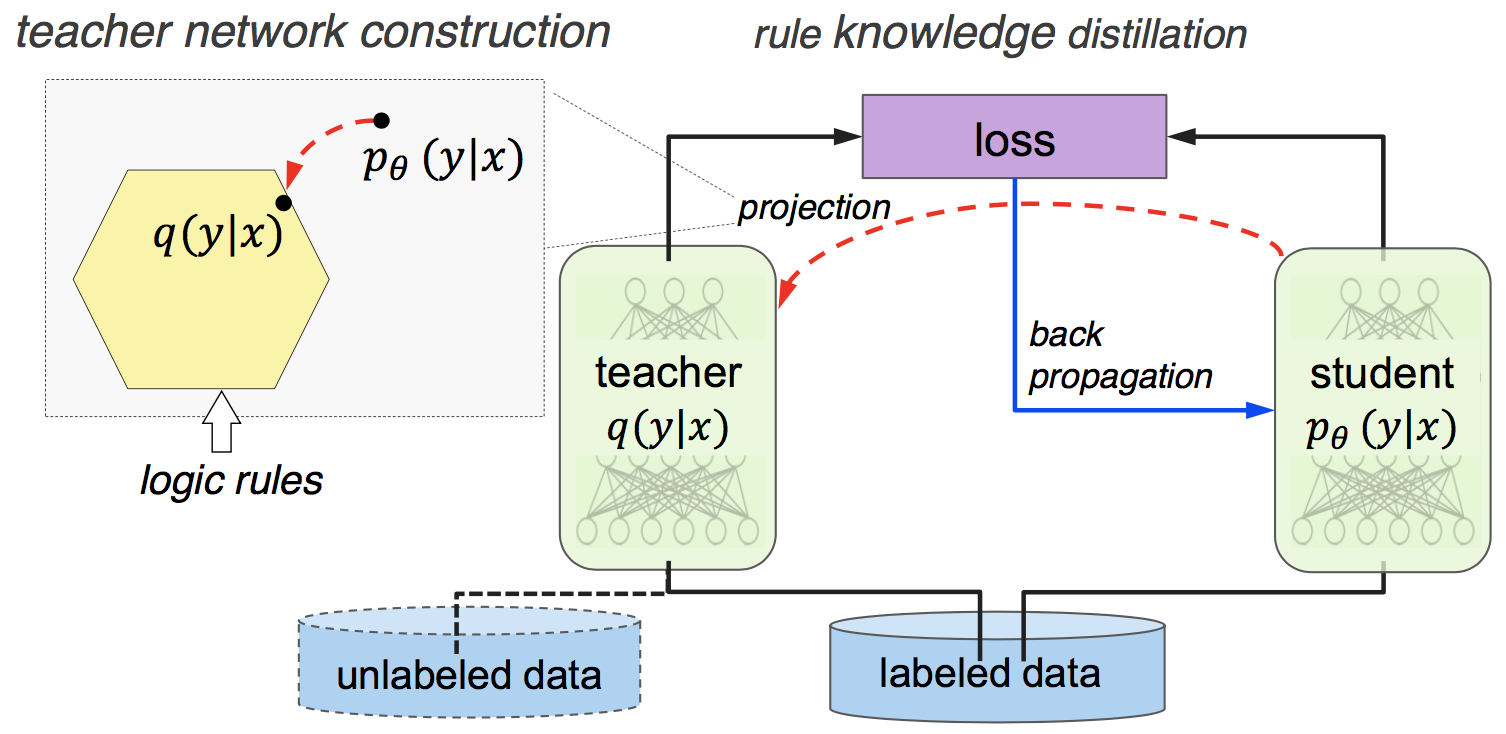
This is pretty neat, but how does one use these soft logical constraints in training deep networks? Harnessing Deep Neural Networks with Logic Rules proposes simultaneously training a student and a teacher network for any classification task with provided PSL rules. The teacher network projects predictions made by the student in a rule regularized space. The student network tries to predict the correct class (cross entropy loss) while also trying to match the predictions of the rule compliant teacher predictions (L2 loss between teacher and student predictions). Given, the student predictions $p_{\theta}(y|x)$ for input $x$, and a set of rules applicable to $x$, \(\{ r_l(x,y)=1 |\; l=1,\cdots,L \}\), the authors find a closed form solution for the projection into the rule constrained space, which is
What has reasoning got to do with intelligence in humans?
To answer this question, it is necessary to understand what is it that humans call intelligence. Intelligence is commonly defined as [7]
The mental ability to learn from experiences, solve problems, and use knowledge to adapt to new situations.
While there seems to be some concensus about its definition, the debate about whether there is one core general intelligence or multiple intelligences seems to be still on. The following short video provides a comprehensive overview of 4 major theories of intelligence in psychology and the ongoing debate.
For the impatient reader who did not watch the video, below I have summarized, the different factors associated with each theory of intelligence. Notice that reasoning appears in some form or the other in each theory. And just from personal experience, most people would agree that intelligent people do effectively apply the knowledge and skills they have already acquired to solve novel problems. But in order to do so they need to be able to decompose any previously solved problem into a sequence of clearly defined and easily executable inference steps. This allows them to recognize previously seen inference steps (or primitive operations) in novel compositional problem structures. And then it is only a matter of executing those inference steps correctly. Hence in some ways reasoning allows for our finite knowledge to be applicable to much larger set of problems than those we have already seen.

Conclusion
In this post our thread of thought began at a layman’s definition of reasoning. We used the layman’s definition to understand reasoning in context of artificial intelligence. There we argued that any reasoning problem can be solved by lookup in a table containing all knowledge man had, has, or will ever seek to have. We acknowledged the practical ridiculousness of this idea and described how math, logic, compositionality, and pattern recognition make the problem more tractable (allowing us to answer more questions from smaller databases). We briefly looked at existing systems that implement some of these ideas. Finally just to mess with your mind, we dabbled in psychology trying to figure out what does reasoning have to do with intelligence in humans. It was a long and winding path. For some of you it might have been a dive into a completely nonsensical rabbit hole. For others it might serve to provide some perspective. Irrespective, feel free to send me an email if you feel strongly about any idea we discussed here, inaccuracies, comments, or suggestions.
